Contributors:

• Juan Carlos Basto Pineda (juan.basto.pineda@gmail.com)
• Diego Rueda

Librería fundamental sobre la cual se construye todo el ecosistema científico y de análisis de datos en Python.

Numpy básicamente ofrece:

• Contenedores homogéneos de datos [arrays]
• Funciones que operan sobre estos contenedores de forma que las operaciones son áltamente eficientes.

Python está organizado en módulos que son archivos con extensión .py que contienen funciones, variables y otros objetos.

Y en paquetes o bibliotecas, que son conjuntos de módulos. Cuando queremos utilizar objetos que están definidos en un módulo tenemos que importarlo.

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

---

Ejemplo 1 - Gráfica simple

"""1. Definimos una función"""
def f(x):
    return (x**3) * (np.cos(x))


"""2. Definimos un dominio X, esto genera un array de numpy,
en este caso un array unidimensional, es decir un vector"""
x = np.arange(-10, 10, 0.1)

# Para limpiar la salida de una celda, selecciónela, digite
# ESC y luego sin soltarlo, pulse la letra R y luego la Y

"""3. Evaluamos la función en el array x"""
y = f(x)

"""4. Mostramos la gráfica"""
plt.plot(x, y, label='$x^3 * cos(x)$')

[<matplotlib.lines.Line2D at 0x7f11706c4c40>]

"""5. Incluir más detalles en la gráfica"""

plt.plot(x, y, label='$x^3 * cos(x)$')
plt.title('Comportamiento de f(x)') 
plt.xlabel('$Dominio$')
plt.ylabel('$Rango_5$')
plt.grid()
plt.legend()
plt.show()

Ejemplo 2 - ¿Por qué usar arrays?

Motivo: Eficiencia

• Los bucles son costosos
• Eliminar bucles, vectorizar operaciones.
• Los bucles se ejecutan en Python, las operaciones vectorizadas en C
• Las operaciones entre arrays de NumPy se realizan elemento a elemento

Ejemplo:

$c_{ij} = a_{ij} + b{ij}$

N,M = 100, 100
a = np.random.rand(10000)
a = a.reshape(N, M) # reshape es un método nativo de los arrays de numpy
b = np.random.rand(10000).reshape(N, M)
c = np.empty([100,100])

%%timeit
for i in range(N):
    for j in range(M):
        c[i,j] = a[i,j] + b[i,j]

%%timeit
c = a + b

¡1000 veces más rápido! Se hace fundamental vectorizar las operaciones y aprovechar al máximo la velocidad de NumPy.

Constantes y funciones universales

Estas funciones operan sobre números y sobre arrays.

np.e

np.pi

np.log(2)

np.sin(np.pi/4)

np.sqrt(2)

np.linalg.norm(a)

¿Qué es exactamente un array?

Un array de NumPy es una colección de N elementos, igual que una secuencia en Python (por ejemplo, una lista). Tiene las mismas propiedades que una secuencia y algunas más. Para crear un array, la forma más directa es pasarle una secuencia a la función np.array

np.array([1, 2, 3, 4, 5])

Los arrays de NumPy son homogéneos, es decir, todos sus elementos son del mismo tipo. Si le pasamos a np.array una secuencia con objetos diferentes, promocionará todos al tipo con más información. Para acceder al tipo del array, podemos usar la función dtype

a = np.array([1, 2, 3.0, 4, 5])
a.dtype

NumPy intentará automáticamente construir un array con el tipo adecuado teniendo en cuenta los datos de entrada, aunque nosotros podemos forzarlo.

np.array([1, 2, 3, 4, 5], dtype=float)

np.array([1, 2, 3, 4, 5], dtype=complex)

También podemos convertir un array de un tipo a otro utilizando el método .astype

a

a = a.astype(int)
a

Atributos y funciones de arrays

Una vez se ha creado un array es posible acceder a información sobre su estado.

# Forma del array
a.shape

# Total de bytes que ocupa este array
a.nbytes

# Número de dimensiones de un array
a.ndim

# Suma de elementos
a.sum()

# Mínimo, máximo y media
a.min(), a.max(), a.mean()

Creación de arrays

1-D:

a = np.array([1, 2, 3])
a

2-D, 3-D, ...

b = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
b

b.ndim

b.shape

Funciones para crear arrays

En la práctica, rara vez creamos los arrays pasando los elementos de uno en uno...

Separación equidistante

np.arange(10)

np.arange(0, 1, 0.2) 

Especificando el número de elementos

np.linspace(0, 1, 10)

Otros arrays comunes

np.ones((3,3))

np.zeros((2,2))

np.eye(4, 4)

np.diag(np.array([1,2,3,4]))

Números Aleatorios

np.random.rand(4)  # Uniforme entre [0, 1]

np.random.normal() # Gaussian de Media 0 y Varianza 1

np.random.normal(loc=0.0, scale=1.0, size=[4,4])

np.random.randint?

np.random.randint(low=1, high=20, size=5)
# Note qué pasa si rodamos esta celda nuevamente

np.random.seed(1234)

np.random.randint(low=1, high=20, size=5)

Las imágenes tambien son arrays!

lena = plt.imread('images/lena.png')
print(type(lena))
print(lena.shape)

lena

Indexado de arrays

Una de las herramientas mas importantes a la hora de trabajar con arrays es el indexado. Consiste en seleccionar elementos aislados o secciones de un array. Nosotros vamos a ver la indexación básica, pero existen técnica de indexación avanzada que convierten los arrays en herramientas potentísimas.

1-D Arrays

a = np.arange(10)
a

a[0], a[2], a[-1]

a[::-1]

Para arrays multidimensionales, los índices son tuplas de enteros según las dimensiones del array.

a = np.arange(16).reshape((4,4))
a

En 2D la primera dimensión corresponde a las filas, la segunda a columnas

a[0, 0]

No solo podemos recuperar un elemento aislado, sino tambien porciones del array, utilizando la sintaxis [<inicio>:<final>:<salto>]

Obtener las dos filas de la mitad

a[1:3:1, :]

Obtener las dos columnas de la mitad

a[:, 1:3:1]

plt.imshow(lena, cmap='gray')

<matplotlib.image.AxesImage at 0x7f11704b1e80>

plt.imshow(lena[128:384, 128:384], cmap='gray')

Operaciones con arrays

Elemento por elemento

Toda la aritmética funciona elemento por elemento

a = np.arange(5)
a

a + 1

b = np.ones(5)
a - b

Esto NO es multiplicación de matrices

c = np.ones(3)
c * c

(para multiplicación de matrices está la función np.malmut, y para producto punto entre vectores np.dot)

Otras operaciones

Comparar arrays

a = np.array([1, 2, 3, 4, 5, 6, 7])
b = np.array([4, 2, 2, 4, 3, 2, 1])

a == b

a > b

Podemos usar estas comparaciones como una mascara para modificar y acceder a los valores que cumplan la condición.

a[a > b] = 0
a

Funciones universales

a = np.arange(5)
a

np.sin(a)

np.exp(a)

Reducciones básicas

1-D arrays

a = np.array([1, 2, 3, 4])

np.sum(a)

a.sum()

Arrays multidimensionales

a = np.arange(9).reshape((3,3))
a

# Primera dimensión
a.sum(axis=0)

# Segunda dimensión
a.sum(axis=1)

Otras reducciones

Funciona de igual manera con el axis y en múltiples dimensiones.

x = np.array([1, 2, 3, 4])
x.min()

x.max()

x.mean()

x.std()

Ejercicios

Ejercicio 1.

1. Crear un array z1 de 3x4 lleno de ceros de tipo entero.
2. Crear un array z2 de 3x4 lleno de ceros salvo la primera fila que serán todo unos.
3. Crear un array z3 de 3x4 lleno de ceros salvo la última fila que será el rango entre 5 y 8

Ejercicio 2.

1. Crea un vector de 10 elementos, siendo los impares unos y los pares doses.
2. Crea un tablero de ajedrez, con unos en las casillas negras y ceros en las blancas.

Puede mostrar el tablero de ajedrez usando plt.imshow(array)

Ejercicio 3.

1. Crea una matriz aleatoria 5x5 y halla los valores mínimo y máximo.
2. Normaliza esa matriz entre 0 y 1

Broadcasting

Las operaciones básicas (suma, resta, etc.) se hacen elemento por elemento y funciona en arrays de diferente tamaño.

La imagen siguiente da un ejemplo de broadcasting

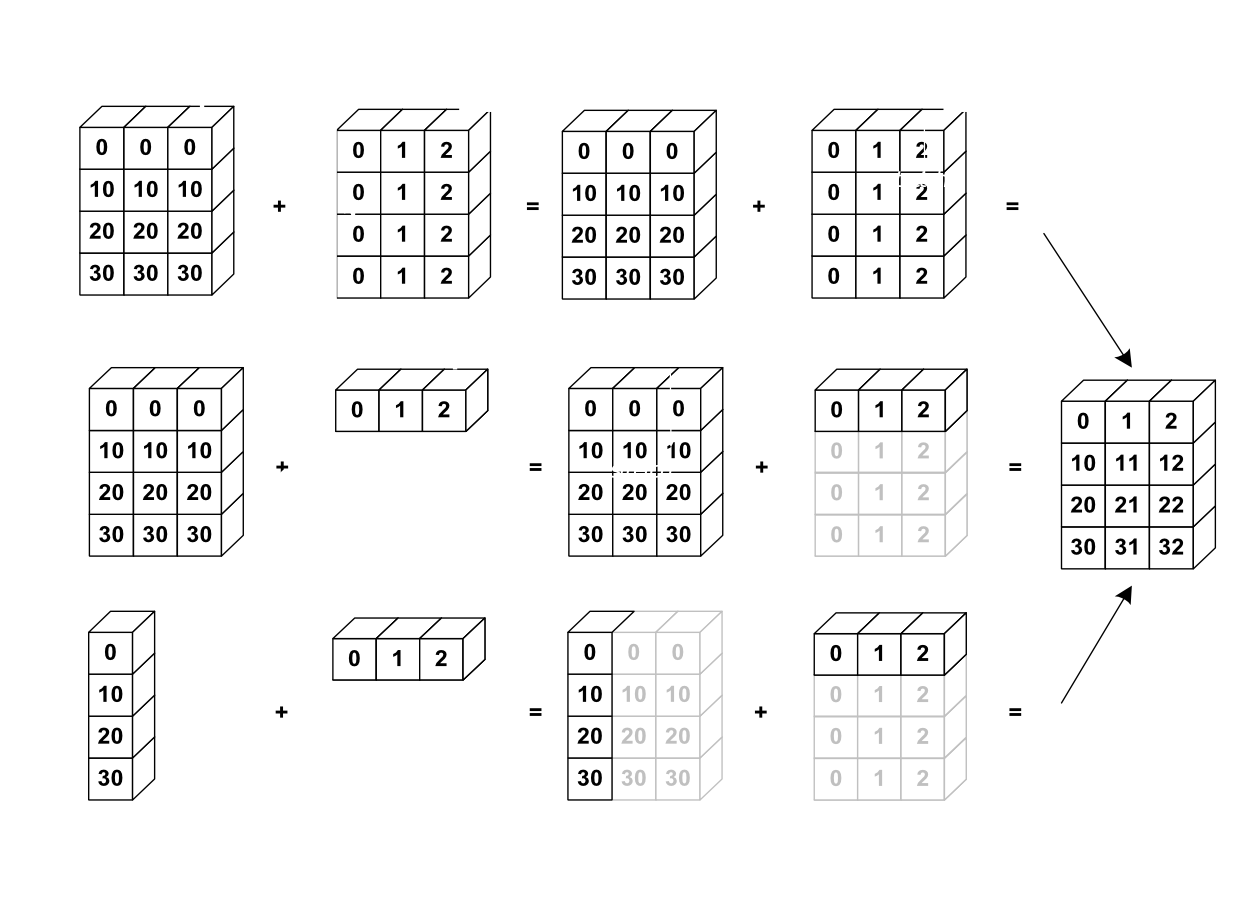
a = np.array([[0], [10], [20], [30]])
a

b = np.array([0, 1, 2])
b

a + b

Manipulación de formas

Colapsar

Reducir una matriz de múltiples dimensiones y la colapsa a una dimensión.

a = np.array([[1, 2, 3], [4, 5, 6]])
a.ravel()

a.T

a.T.ravel()

Reformar

La operación inversa a colapsar.

b = a.ravel()
b

b.reshape((2,3))

b.reshape((3,2))

Manejo de Archivos

Tablas

Demos una mirada al archivo /data/populations.txt

year	hare	lynx	carrot
1900	30000	4000	48300
1901	47200	6100	48200
1902	70200	9800	41500
1903	77400	35200	38200

# Leer datos desde archivo
data = np.loadtxt('data/populations.txt')
data

Ejercicio:

Genere un gráfico para observar el cambio en la población de liebres y de linces a lo largo de los años

# Almacenar datos en formato texto

# Suponga que se ha cometido un error, y los datos de población de linces,
# reportados en miles, se trataba en realidad de centenares. Corrija la
# columna respectiva y almacene la tabla con un nuevo nombre utilizando:

np.savetxt('data/pop2.txt', data, fmt='%5.i',  delimiter='\t')

Formato Numpy

Numpy tiene su propio formato binario.

data = np.ones((3,3))
data

np.save('data/ones.npy', data)

data3 = np.load('data/ones.npy')
data3

Resumen

• Sabe crear arrays: array, arange, ones, zeros, rand
• Conoce la forma de un array shape y los diferentes métodos de indexado para obtener diferente secciones del array array[::2], etc.
• Ajustar la forma de un array usando reshape o aplanarla con ravel
• Obtener un subconjunto de elementos de un array y modificar sus valores usando mascaras a[a < 0] = 0
• Conocer operaciones miscelanes con arrays, encontrar el máximo array.max() o la media array.mean(), entre otras.
• Tiene una idea básica del broadcasting y sus reglas.

Análisis de Vinos

Usando los resultados de un análisis químico de vinos obtenidos de la misma región en Italia pero de tres diferentes cultivos. Examine el archivo data/wine.csv.

Los atributos del dataset son:

1. Wine (Class)
2. Alcohol
3. Malic acid
4. Ash
5. Alcalinity of ash
6. Magnesium
7. Total phenols
8. Flavanoids
9. Nonflavanoid phenols
10. Proanthocyanins
11. Color intensity
12. Hue
13. OD280/OD315 of diluted wines
14. Proline

---

Truco:

Use np.set_printoptions(suppress=True, precision=3) para imprimer los datos de una manera mas legible.

Ejercicios

1. Lea los datos desde la ruta data/wine.csv, use el parámetro delimiter=',' para valores separados por coma.
2. Determine entre las 3 clases de vinos, cual tiene el mayor promedio de Alcohol.
3. Un vino con concentración de ácido málico mayor a 3.5 se considera demasiado maduro, cuántos vinos tienen una concentración mayor?
4. Usando el comando plt.hist(array) cree un histograma de ácido málico.
5. Normalice entre [0,1] los datos de Alcohol e Intensidad de Color
6. Usando el comando plt.scatter(array1, array2) cree un gráfico de dispersión de las dos columnas normalizadas.

np.set_printoptions(suppress=True, precision=3)

array([[   1.  ,   14.23,    1.71, ...,    1.04,    3.92, 1065.  ],
       [   1.  ,   13.2 ,    1.78, ...,    1.05,    3.4 , 1050.  ],
       [   1.  ,   13.16,    2.36, ...,    1.03,    3.17, 1185.  ],
       ...,
       [   3.  ,   13.27,    4.28, ...,    0.59,    1.56,  835.  ],
       [   3.  ,   13.17,    2.59, ...,    0.6 ,    1.62,  840.  ],
       [   3.  ,   14.13,    4.1 , ...,    0.61,    1.6 ,  560.  ]])

Contributors:

• Juan Carlos Basto Pineda (juan.basto.pineda@gmail.com)
• Diego Rueda